Farene ved lineær tenkning i ledelse

Vi antar altfor ofte at det er lineære sammenheng i arbeidslivet. I noen tilfeller er det riktig: Øker du lagerstørrelsen med 50 prosent, får du plass til 50 prosent flere varer på hyllene. Gir du alle ansatte 10 prosent lønnsøkning, vil de totale lønnskostnadene øke med 10 prosent. Men i andre tilfeller er ikke sammenhengen lineær, og det er her lineær tenkning kan få dramatiske konsekvenser.

Ledere som ikke vet om sammenhengen er lineær eller ikke-lineær, kan fatte beslutninger som kan få dramatiske konsekvenser for lønnsomheten i virksomhetene de leder. I dette blogginnlegget viser jeg praktiske eksempler på ikke-linearitet som du bør være klar over. 

Besparelser ved drivstofforbruk

La oss si at du sitter som økonomisjef og har ansvar for to varebiler. Bilene har en årlig kjørelengde på 10 000 mil (dette eksemplet er inspirert fra en artikkel i HBR mai-juni 2017 (artikkelen kan kjøpes, om du ikke er abonnent da):

• A kan kjøre 6,7 km pr liter. Her har du fått et tilbud på en nyere modell som kan kjøre 10,0 km pr liter
• B kan kjøre 12,5 km pr liter. Her har du fått et tilbud på en nyere modell som kan kjøre 25 km pr liter

Du har bare anledning til å bytte én bil. Hvilken er mest lønnsom å bytte, forutsatt at drivstofforbruket er den eneste parameteren du vurderer?

Mange vil her oppfatte Alternativ B som et bedre alternativ, fordi du kan kjøre dobbelt så langt per liter. Overraskelsen for mange er at Alternativ A er det beste valget. Du sparer 5000 liter i året sammenlignet med 4000 liter i året for Alternativ B:

Drivstofforbruk er ikke en lineær funksjon av antall mil pr liter. Grafen nedenfor illustrerer dette.

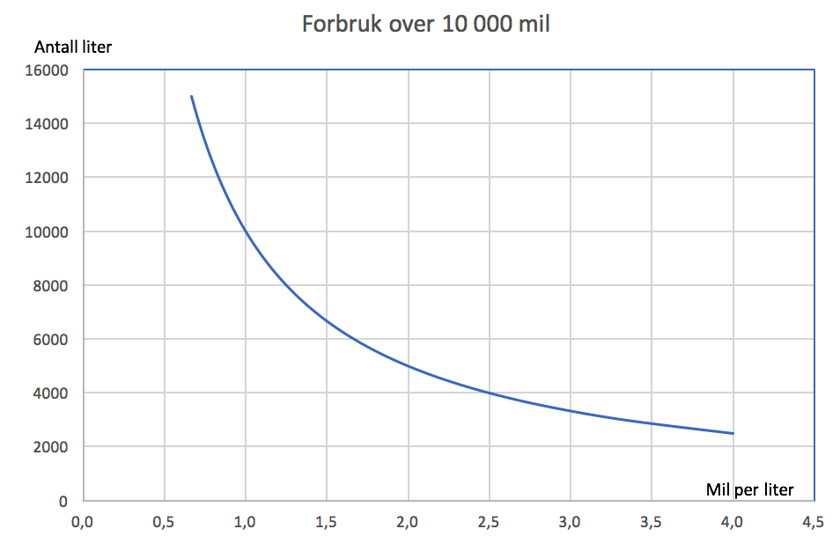
Grafen viser antall liter i forbruk målt mot antall kjørte mil per liter (x-aksen)

Pris-/volumkombinasjoner er ikke lineære

Et annet område hvor mange har en tendens til å tenke linearitet er på kombinasjonen pris og volum. Det er fristende å sette ned prisen for å øke salgsvolumet. Jeg skal her vise at prisendringer har langt større effekt på lønnsomheten enn volumendringer. 

La oss si at du selger DAB-radioer i nettbutikken din. Du har i utgangspunktet en utsalgspris på 2 000 kroner og variable kostnader på 1 000 kroner per radio. Du har prognoser på at dette vil gi deg et salgsvolum på 10 000 enheter i løpet av året og et budsjettert overskudd på 10 millioner kroner.

På mandagens ledermøte legger salgssjefen fram et forslag til to kampanjer: 

• Kampanje A er en rabatt på 25 % med forventet salgsøkning på 50 %
• Kampanje B er en rabatt på 40 % med forventet salgsøkning på 100 %

Det er fristende å gå for Kampanje B, som du antar vil gi en dobling av salgsvolumet. Men før du beslutter, bør du ta hensyn til marginene på salget. Vi forutsetter at kampanjen ikke innebærer endringer i de variable kostnadene. I realiteten vil kostnadene bli høyere, gitt at du ønsker å kjøre annonsering av den nye kampanjen.

Verken Kampanje A eller B er lønnsomme sammenlignet med normalprisingsalternativet.

I grafen nedenfor vil du se effekten av prisendringer på nødvendig salgsvolum om målet fremdeles skal være minst 10 millioner kroner i overskudd på radiosalget.

Kampanje B, med 40 % rabatt, vil kreve et salgsvolum på minst 50 000 enheter, eller en salgsøkning på 400 %. 

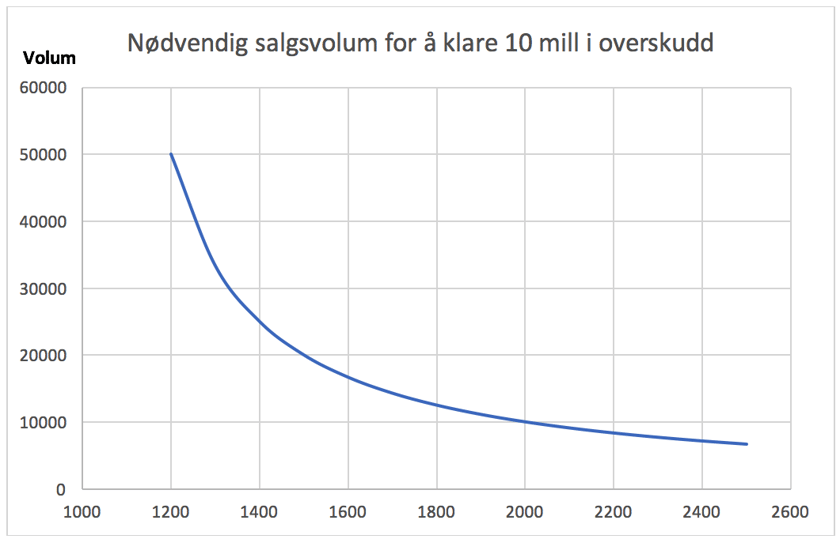
Grafen viser salgsvolum mot pris (x-aksen)

Kundeatferd er ikke-lineær

Konsumenters holdninger og atferd følger heller ikke en lineær kurve. Det er gjort mange undersøkelser rundt konsumenters atferd rundt priser, avgifter, lojalitet og holdninger til sikkerhet, trusler og miljø.

En grov feilkilde er problemet med gjennomsnittsbetraktninger. Gitt at du måler kundetilfredshet på en skala fra 1 til 5, hvor 1 er meget utilfreds og 5 er meget tilfreds. Dette er en altfor grov skala til å gi nyttig beslutningsgrunnlag til ledelsen. Gitt at du får gjennomsnittsmåling på 4,1. Er faren da over? Langt i fra! Forskjellen mellom 3 og 4 kan være ubetydelig. Du kan få feilkilder ved at noen respondenter trekkes mot midten av skalaen – de benytter ikke hele skalaen.

Les også: Hvorfor du bør måle kundetilfredsheten og hvordan du gjør det

Kundelojalitet er ikke-lineær

Gitt at du som salgssjef har to forskjellige markedssegmenter som begge gir et årlig bidrag på 1000 kr: 

• Segment A har en lojalitetsgrad på 30 %, men du antar du kan øke denne til 60 % med en investering på 100 kr
• Segment B har en lojalitetsgrad på 80 %, men du antar at du kan øke denne til 90 % med en investering på 200 kr

Hvilket alternativ er mest attraktivt?

Segment A: KLV øker fra 376 kr til 1200 kr, det vil si med 824 kr
Segment B: KLV øker fra 2667 kr til 4500 kr, det vil si med 1833 kr

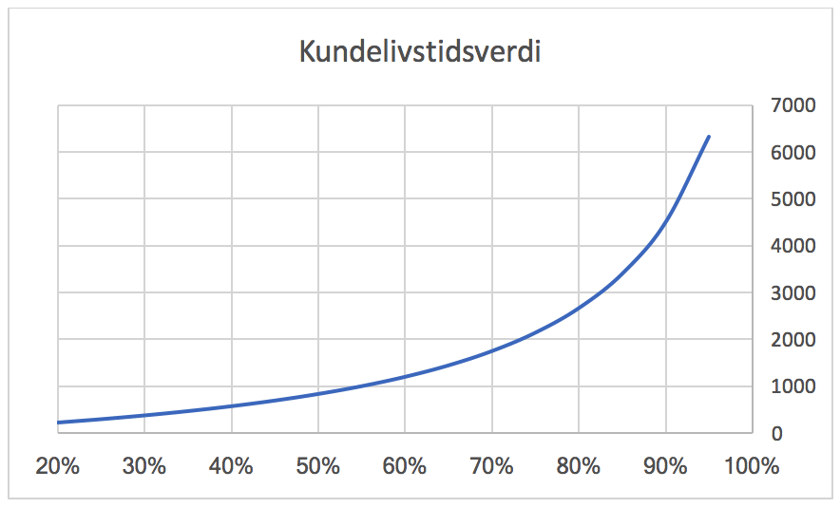
Grafen viser kundelivstidsverdi mot lojalitetsgrad (x-aksen). 

Hva kan du lære av ikke-lineær tenkning?

Du vil lære at selv små justeringer kan gi svært gode resultater, men du må vite hvor på skalaen du befinner deg. Lineær tenkning gjør at ledere ofte overser effekten av små endringer på høye lojalitetsgrader.

Du bør også se opp for gjennomsnittsmålinger og hvordan skalaen er satt opp: I en skala fra 1 til 5, hvor 5 er svært tilfreds, vil du først se vesentlige resultater ved en endring fra 4 til 5. 5-ere er typiske ambassadører for dine produkter. Det er lettest å få dine kolleger til å forstå ikke-lineære sammenhenger om du visualiserer gjennom grafer, som vist i dette innlegget.

Hva bør du som leder gjøre nå?

Du bør sikre at ledergruppen er klar over konsekvensene av lineær tenkning på områder som er ikke-lineære. Du bør kartlegge de områdene du mener kan være ikke-lineære. Finn deretter ut hva slags ikke-linearitet du har med å gjøre. Kurvene kan i noen tilfeller være motsatte av eksemplene jeg har vist her. Noen stiger raskt for deretter å flate ut. Andre kan være stabilt høye opp til en verdi, for deretter å falle dramatisk.

Dersom du kjører feltstudier: Husk å teste på minst tre kombinasjoner av verdier. To kombinasjoner vil gi en rett linje. Du er avhengig av minst tre for å se hvordan sammenhengen er.

Først publisert 31. mai 2017. Oppdatert 25. juli 2018.